Value Function Approximation

• Value Function Approximation
• Intro
• Supervised Learning Formulation
• Estimating Target Value
• TD(λ)
• LSPI

Intro

• Tabular methods use discrete space
• This might be infeasible for big environments
• It is basically ML

Supervised Learning Formulation

To use RL with this we need to find a parameter vector that represents the data. This can be achieved with supervised learning. We need to minimize the error of the parametrized value function V(s;θ):

This can be done analytically with the partial derivative 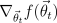gradient:

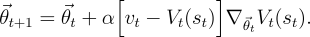
Estimating Target Value

The target value might not be the true value of 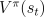but a noisy version of it.

TD(λ)

Here V is implicitly a function of θ

LSPI

• Least-Squares Policy Iteration
• source: https://www.cs.duke.edu/research/AI/LSPI/jmlr03.pdf
• RL for control
• model-free
• off-policy
• uses LSTD (Least-Squares Temporal-Difference)
• separation of sample collection and solution

function LSPI-TD(D, π0)
  π' <- π0
  repeat
    π <- π'
    Q <- LSTDQ(π, D)
    for add s in S do  # simple greedy policy based on Q
       π'(s) <- argmax Q(s, a)
  until π ~ π'
  return π